高校の数学で習うサイクロイドのうち、外サイクロイド(エピサイクロイド)と呼ばれるものを今日は取り扱います。
さて、これをなぜ題材にしたかというと、ある生徒を指導しているときに、
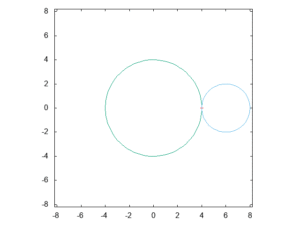
「半径2cmの円が、半径4cmの円の外側に沿ってすべらないように転がっていきます。さて、半径2cmの円が、半径4cmの円の周りを一周して、もとの位置に戻ったとき、半径2cmの円は何回転しましたか。」
という問題に当たったからです。さて、答えは何回転だと思いますか?なお、下の図は、問いを図示したものです。
(GIF動画、クリックで動画再生)
では図を無視してまずは計算してみましょう。半径2cmの円の周の長さは4×3.14=12.56cmですね。一方、半径4cmの円の周の長さは4×3.14=25.12cmです。だから答えは、これらの長さを比較して2回転!ではありません。
例えば、「平らな面で考えた場合。半径2cmの円が平らな面上をすべらずに転がります。転がった距離が25.12cmだったとき、円は何回転しましたか。」という問いだと、答えは2回転です。しかし、円周上を円がすべらずに転がる場合は、半径4cmの円周上を1回転している分を別に足さなければなりません。したがって、もともとの問いの答えは3回転になります。要は、平面だったら2回転だけど、円周上を1回転したのだからもう1回転足さなきゃならないということです。
しかし、この説明はあまりに概念的です。数学的に理屈が通っているか、式を使って説明してほしいという方もいらっしゃることでしょう。
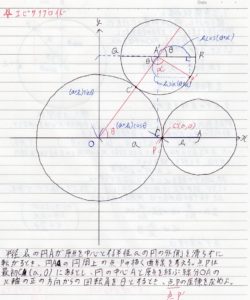
そこで、数学的にはどのように考えればよいかを下に解説してみました。(レベル的には高校3年レベルですが、一応三角関数の導入を添付しておきましたので、深く考えなければ中学生でもわかるようにした「つもり」です。)
(1枚目、クリックで拡大)
(2枚目、クリックで拡大)
以上のとおりですが、注目してほしいのは一番下の式の「動円の回転角」というやつです。
( a + b ) θ / b
あるいは、一つ上の式に
θ + (a / b) θ ・・・式1
とあります。
式1を見てください。例えば、問いにあるとおり、外周を1回転するとは、θ=360度です。a, bは問いに当てはめると、a=4 , b=2です。
したがって、回転角はθ + (a / b ) θ = 360 + 4 × 360 ÷ 2 =360 + 720 = 1080
答えは3回転。初めに説明していた「円周上を1回転するのだから、1回転足す」とは、式1中の1項目、「θ」にあたります。
まぁ、ここまでお読みくださった方は正直お疲れさまでした。数学的に説明せよとなると実は小中学生には非常に難解なものになってしまうのです。だから、問いにあるような回転数の答えはθ + (a / b) θで、θは円周上の角度(円周上を1回転したなら360度)と覚えてしまうほうが楽ですね。
ちなみに、エピサイクロイドの軌跡は、実は結構きれいです。
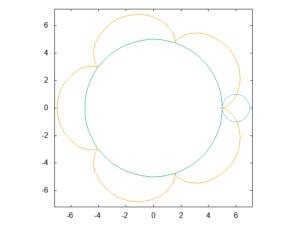
たとえば、a=5,b=1なら、
(GIF動画、クリックで動画再生)
こんな風に、ヒマワリのイラストみたいな感じで図形を描くことができます。
面白い。